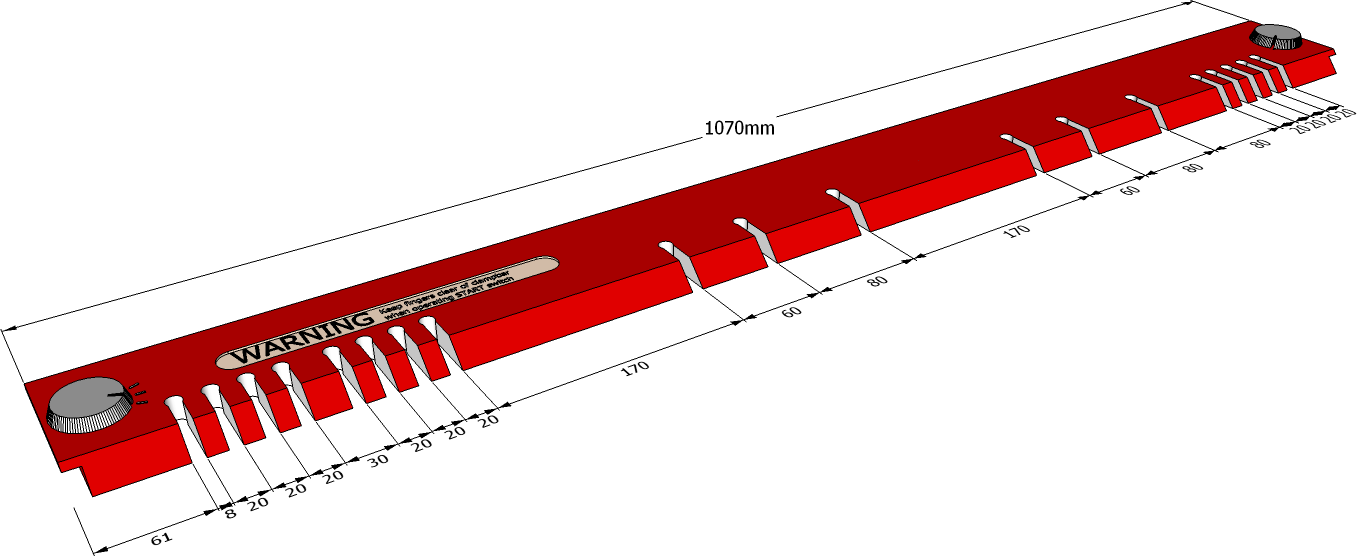
ჩაჭრილი სამაგრი: აქსესუარი Magnabend ფურცლის ლითონის მოსახვევი მანქანებისთვის
ჩაჭრილი სამაგრი იდეალურია არაღრმა უჯრებისა და ტაფების სწრაფად და ზუსტად დასამზადებლად.
ჩაჭრილი სამაგრი აქსესუარი მაგნაბენდის ფურცლისთვის
ჩაჭრილი სამაგრის უპირატესობები უჯრების დასამზადებლად მოკლე სამაგრების კომპლექტთან შედარებით არის ის, რომ მოსახვევი კიდე ავტომატურად სწორდება დანარჩენ მანქანასთან და სამაგრი ავტომატურად აწევს სამუშაო ნაწილის ჩასმას ან ამოღებას.(არანაკლებად, მოკლე დამჭერები შეიძლება გამოყენებულ იქნას შეუზღუდავი სიღრმის უჯრების შესაქმნელად და, რა თქმა უნდა, უკეთესია რთული ფორმების შესაქმნელად.)
გამოყენებისას, სლოტები ექვივალენტურია ჩვეულებრივი ყუთისა და ტაფის დასაკეცი აპარატის თითებს შორის დარჩენილი ხარვეზებისა.სლოტების სიგანე ისეთია, რომ ნებისმიერი ორი სლოტი მოერგება უჯრებს 10 მმ ზომის დიაპაზონში, ხოლო სლოტების რაოდენობა და მდებარეობა ისეთია, რომ ყველა ზომის უჯრისთვის ყოველთვის შეიძლება მოიძებნოს ორი სლოტი, რომელიც მოერგება მას. .
| ჩაჭრილი სამაგრის სიგრძე | კოსტიუმების მოდელი | აყალიბებს სიგრძის უჯრებს | უჯრის მაქსიმალური სიღრმე |
| 690 მმ | 650E | 15-დან 635 მმ-მდე | 40 მმ |
| 1070 მმ | 1000E | 15-დან 1015 მმ-მდე | 40 მმ |
| 1320 მმ | 1250E, 2000E, 2500E & 3200E | 15-დან 1265 მმ-მდე | 40 მმ |
არაღრმა უჯრის დასაკეცი:
დაკეცეთ პირველი ორი მოპირდაპირე მხარე და კუთხის ჩანართები ჩაჭრილი სამაგრის გამოყენებით, მაგრამ ჭრილობების არსებობის უგულებელყოფით.ამ სლოტებს არ ექნება რაიმე შესამჩნევი ეფექტი დასრულებულ ნაკეცებზე.
ახლა აირჩიეთ ორი სლოტი, რომელთა შორისაც უნდა დაიკეცოთ დარჩენილი ორი მხარე.ეს არის რეალურად ძალიან მარტივი და საოცრად სწრაფი.უბრალოდ გაანაწილეთ ნაწილობრივ დამზადებული უჯრის მარცხენა მხარე მარცხენა ყველაზე სლოტით და ნახეთ, არის თუ არა სლოტი მარჯვენა მხარისთვის, რომ შეიყვანოთ;თუ არა, გაასრიალეთ უჯრა გასწვრივ მანამ, სანამ მარცხენა მხარე არ იქნება შემდეგ ჭრილში და სცადეთ ხელახლა.როგორც წესი, დაახლოებით 4 ასეთი მცდელობა სჭირდება ორი შესაფერისი სლოტის მოსაძებნად.
ბოლოს, უჯრის კიდეზე სამაგრის ქვეშ და ორ არჩეულ ჭრილს შორის გადაკეცეთ დარჩენილი მხარეები.ადრე ჩამოყალიბებული მხარეები გადადის შერჩეულ სლოტებში, როდესაც საბოლოო ნაკეცები დასრულდება.
გამოქვეყნების დრო: მაისი-16-2023